Расчет годовых процентов: формула, правила расчета и примеры расчетов
Расчет годовых процентов производится для выяснения размера вознаграждения как по депозиту, так и по кредиту. Техника подсчета используется в целом во всех сферах финансового сектора.
Если вы решили приумножить свои сбережения, то лучше провести анализ кредитных организаций и выбрать наиболее подходящий вариант. Для этого нужно знать критерий выделения прибыльного предложения. В этом поможет оценка ставки.
Как рассчитать процентную ставку: годовую или месячную

Зачастую на сайтах организаций есть специальный калькулятор, с помощью которого можно узнать доходность вклада. Что же делать, если такой функции на сайте не представлено? Да и в договоре вряд ли будет стоять ссылка на результаты подсчета, сделанные калькулятором. Его можно изменить или вообще убрать. Лучше всего производить вычисления самому.
Расчет процентов по годовой ставке включает в себя формулу простого и сложного процента. Она указывается в документах и может быть фиксированной и плавающей. С последней иметь дело сложнее, так как она трудно прогнозируется. В этом случае базой для плавающей ставки может быть какой-нибудь ключевой параметр, например, ставка рефинансирования ЦБ. При ее изменении с определенным лагом меняется и плавающая ставка. Фиксированная же ставка привносит больше легкости в сравнительный анализ и общее понимание.
Способ расчета простого процента
Простой процент – это процент по вкладу или кредиту, имеющий указанные в договоре периодичность и срок выплат, но без включения начисленных процентов в предыдущем периоде. Расчет годового процента по кредиту аналогичен подсчетам, проводимым по депозиту. На картинке ниже представлена формула, где Р – это тело кредита, а S – начисленные проценты. В обычной практике приравнивают количество дней в году к 365 или 366 (редко к 360), а в месяце к 30 дням.

Исходя из формулы, можно заметить, что сумма простого процента находится в зависимости от процентной ставки и срока вклада. Однако фактор периодичности начисления совершенно не имеет влияния на конечную доходность. Это объясняется тем, что проценты не присоединяются к основной сумме вклада.
В свою очередь, если в условиях договора указано, что проценты выплачиваются с определенной периодичностью, а не по завершении срока, то итоговая доходность равна сумме процентов. Примером служит ежемесячное начисление.
Пример использования простых процентов
Условие задачи № 1
Клиент обратился в банк с просьбой о размещении вклада со сроком на полгода. Для 6 месяцев депозита предусмотрена ставка 8,7 % годовых с ежемесячным начислением. Минимальная сумма для совершения сделки: 30 000 рублей.

Итак, взаимодействуя с банком на предъявленных условиях, получаем:
Сумма процентов = 30 000 х 181 х 8,7 : (100 х 365) = 1294,3 руб. Надо отметить, что расчет годового процента по кредиту выглядел бы совершенно таким же образом.
Но в связи с тем, что в условии сказано о ежемесячной выплате процентов, полученная сумма будет осуществлена шестью платежами. Количество календарных дней влияет на размер этих самых выплат. Допустим клиент обратился в декабре, тогда:
- Проценты за декабрь, январь, март, май = 30 000 х 31 х 8,7 : (100 х 365) = 221,67 руб.
- Проценты за февраль = 30 000 х 28 х 8,76 : (100 х 365) = 200,22 руб.
- Проценты за апрель = 30 000 х 30 х 8,7 : (100 х 365) = 214,52 руб.
В итоге за 6 месяцев сумма депозита или кредита с начисленными процентами составит:
- Сумма с процентами = 30 000 х (1 + 181 х 8,7 : (100 х 365)) = 31 294,274 руб. Или просто 30 000 + 1294,3 = 31 294,3 руб.
Способ расчета сложного процента
Плата за пользование полученными деньгами (в случае кредита) и вознаграждение за передачу собственных средств на хранение (в случае депозита) в основном вычисляются с помощью второго вида доходности. Расчет годовых процентов сложного типа включает в себя процент, учитывающий как начисление на сумму вклада, так и сумму ранее начисленных по вкладу процентов. При этом периодичность и срок договора также входят в условия расчета капитализированного процента. Ниже представлена формула расчета суммы процентов. Годовые значения имеют наращенный характер. Далее представлено на примере, какой из методов начисления процентов является наиболее выгодным для потребителя.

Формула расчета годовых процентов показывает, что вклад или кредит с капитализацией обязательно должен иметь периодичное начисление процентов. Это приводит к тому, что разбитый на периоды срок банковского договора способствует начислению процента за каждый временной промежуток с последующей капитализацией. Месяц выступает в роли наиболее популярного периода причисления процента, доход которого определяется по календарным дням. Поэтому совокупная прибыльность вклада выводится по сумме процентов, начисленных по отдельным периодам.
Пример использования сложных процентов
Далее выведем прибыльность сберегательного вклада с тем же условием, как и в предыдущем примере. Исключение составляет применение метода капитализированного процента.
Задача № 2
Условия депозита:
- Вложение - от 30 000 рублей.
- Депозитный срок - 6 месяцев (декабрь-май).
- Периодичность начисления и выплаты процентов - ежемесячно с капитализацией.
- Ставка по вкладу - 8,7 % годовых.
Алгоритм расчета приведен в таблице ниже.
| Месяц | Сумма, рублей | Количество дней | Проценты | Итог по месяцам, рублей |
| 1-й месяц | 30 000 | 31 | 8,7 : (100 х 365) | 221,67 |
| 2-й месяц | 30 000 + 221,67 | 31 | 8,7 : (100 х 365) | 223,31 |
| 3-й месяц | 30 221,67 + 223,31 | 28 | 8,7 : (100 х 365) | 203,19 |
| 4-й месяц | 30 444,98 + 203,19 | 31 | 8,7 : (100 х 365) | 226,46 |
| 5-й месяц | 30 648,17 + 226,46 | 30 | 8,7 : (100 х 365) | 220,77 |
| 6-й месяц | 30 874,63 + 220,77 | 31 | 8,7 : (100 х 365) | 229,77 |
В итоге спустя полгода сумма сложных процентов стала равной 1325,17 руб., итоговая сумма вклада с процентами - 31 325,17 руб. Таким образом, вклад с капитализацией процентов за 6 месяцев принес дополнительный доход в размере 30,87 руб.
Расчет годового процента по займу производился бы тем же путем. В ситуации взятия кредита или обращения в мелкие финансовые организации, такие как МФО, процентные начисления производятся таким же способом. Отличие заключается в формулировке названия. В случае депозита – это доходность, в случае кредита – это комиссии клиента или доходность самого банка.
Основные правила начисления вознаграждения
Финансовые вычисления включают в себя также анализ инвестиционного процесса. Ведь годовые проценты применяются не только для расчета традиционных методов сохранения средств, то есть для сберегательных вкладов, но и для оценки инвестиций на фондовом рынке. Ниже представлены основные принципы расчета, относящиеся ко всем типам приумножения капитала.
Если процент – это денежные поступления в качестве дохода, то простой и сложный процент – это ставки, по которым этот доход начисляется с определенной периодичностью на тело вклада или долга. При рассмотрении двух видов процента можно заметить, как индивид получает большую доходность, если банк используется сложные проценты. Это связано с постоянным реинвестированием накопленного дохода.

Изменение стоимости денег во времени
Как связаны временная денежная стоимость и расчет годовых процентов ? Дело в том, что процесс начисления процентов увеличивает первоначальную сумму свободных финансовых средств. Чтобы выбрать из нескольких вариантов инвестирования, нужно проводить анализ доходностей активов. Особенность заключается в разных периодах поступления дивидендов. Для сравнения их приводят к одному временному периоду. Ниже приведены примеры.
Пример будущей стоимости денег
Задача № 3
Найти будущую стоимость (БС) актива, если планируется вложение 5000 рублей, под 10,5 % годовых на 3 года.
В этой задаче текущей стоимостью (ТС) будет являться 5000 рублей, а БС этих же средств рассчитывается двумя способами. Первый без реинвестирования, а второй с учетом реинвестирования данных средств. Тогда данные расчеты выступают аналогом простых и сложных процентов.
Формула использования сложных процентов выглядит следующим образом:
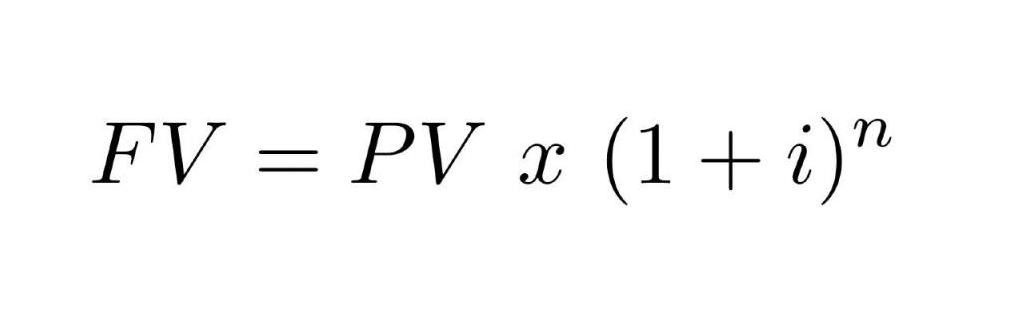
Где:
- FV (англ. Future Value) - будущая стоимость денег.
- PV (англ. Present Value) - текущая или первоначальная стоимость.
Использование простых процентов выглядит так же, но записанная в скобки ставка процентов не возводится в степень, а умножается непосредственно на количество периодов.
Тогда в задаче, представленной выше, БС с применением простых процентов будет равна:
- FV = 5000 х (1 + 5 х (10,5 : 100)) = 5000 х 1,525 = 7625.
А с применением сложных процентов иначе:
- FV = 5000 х (1 + (10,5 : 100))^5 = 5000 х 1,647 = 8235.
Разница в доходности составит 610 рублей. Отсюда, взаимодействовать с финансовыми организациями, использующими сложные проценты для своих расчетов, намного выгоднее.
Чтобы сравнить денежные притоки по инвестициям, которые осуществляются в разные сроки, нужно привести их к одному моменту времени. Эта процедура называется дисконтированием, если финансовые поступления приводятся к начальному периоду, и наращением, если к будущему моменту времени. Однако в обоих случаях формула расчета процентов не изменяется. Меняется только расположение процентного множителя.
Использование Excel для подсчета
Использование компьютерной программы для произведения расчетов является более выгодной стратегией. Автоматизация вычисления позволяет быстро обработать большое количество материала.

Вбивание формул простых и сложных процентов упрощает процедуру калькуляции. Для этого не нужно каждый раз ее прописывать, достаточно вбить и протянуть формулу по ячейкам, чье количество равно числу периодов. Тем самым облегчается процесс анализа инвестиционных стратегий или выбор банковских предложений.
