Кластеризация - это... Методы кластеризации

Кластеризация - это статистический метод, заключающийся в разбивке данных на группы, называемые кластерами. В каждой из них объекты должны иметь сходства по какому-либо критерию. Одновременно нужно, чтобы данные из разных групп максимально различались. Можно сказать, что кластеризация - это синоним понятия "кластерный анализ".

Зачем нужен этот метод

С помощью кластерного анализа выявляются структурные группы для лучшего понимания информации. Кроме того, он позволяет упрощать обработку данных. Использование метода кластеризации актуально и для больших, и для малых объемов информации. Он способствует компактному хранению сведений и поиску атипичных объектов, не вошедших ни в одну группу.

Сферы применения

Кластеризация - это способ обработки данных, применимый во многих отраслях: в биологии, медицине, маркетинге, биоинформатике, экономике, социологии, археологии. Использование данного метода уместно, когда систематизируется большое количество информации для упрощения дальнейшей работы. Исследователям нужно знать, что такое кластеризация, и уметь применять ее принципы. Метод отлично себя зарекомендовал.

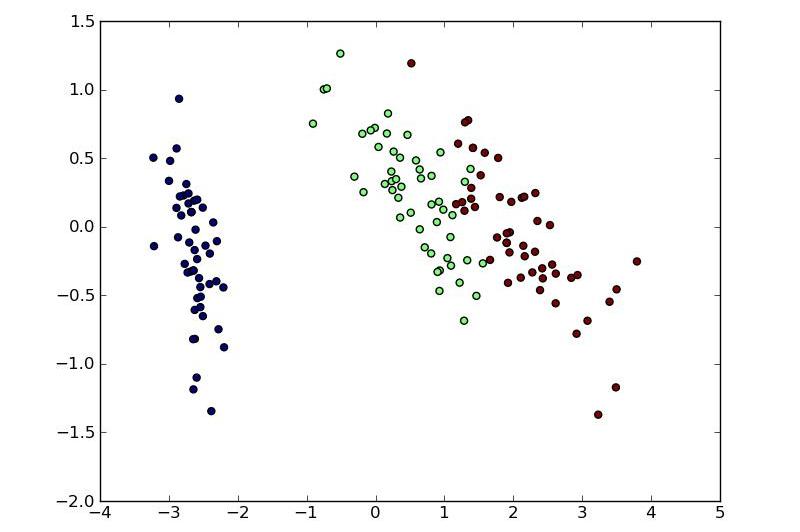
Алгоритмы кластеризации

Последовательность команд в общем виде выглядит следующим образом:

Отбор объектов кластеризации.
Подготовка данных путем приведения к нужному виду.
Вычисление коэффициента сходства.
Выбор алгоритма кластерного анализа.
Реализация алгоритма.
Интерпретация результатов.

Выбор алгоритма - задача не из легких. Тут необходимо учитывать множество факторов. Часто приходится использовать несколько алгоритмов подряд или их комбинацию (метаалгоритм) для получения оптимального результата.

Для всех пар объектов измеряются расстояния (степени сходства). Они определяются в одномерном или многомерном пространстве. Быстро и просто узнать данный параметр между объектами в многомерных пространствах можно путем вычисления евклидовых расстояний. Это не очень сложно. В двух- или трехмерном пространстве эта мера - действительное геометрическое расстояние между объектами. При этом алгоритм не распознает, реальны определенные величины или исследователь имеет дело с их производными. В таком случае необходимо подобрать правильный метод, отталкиваясь от специфики работы.

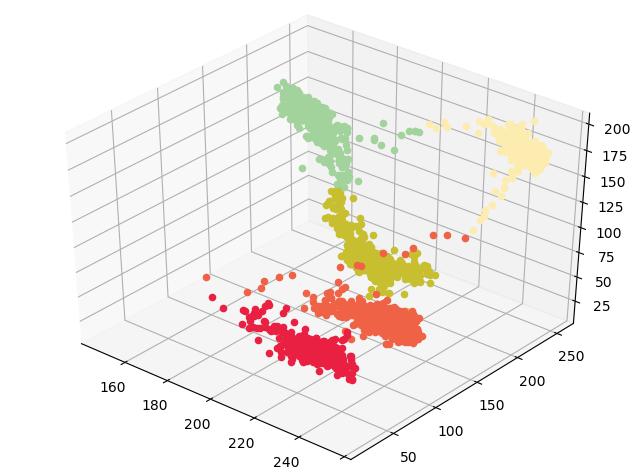
Алгоритмы кластерного анализа подразделяются на иерархические и неиерархические. При этом данные первого типа в конце генерируют иерархию кластеров. Любой из них может быть использован для интерпретации результатов.

Иерархические алгоритмы

Иерархическая кластеризация - это алгоритм, строящий разветвленную систему разбивки выборки на группы. Не требуется предварительно указывать количество кластеров, которые будут генерироваться.

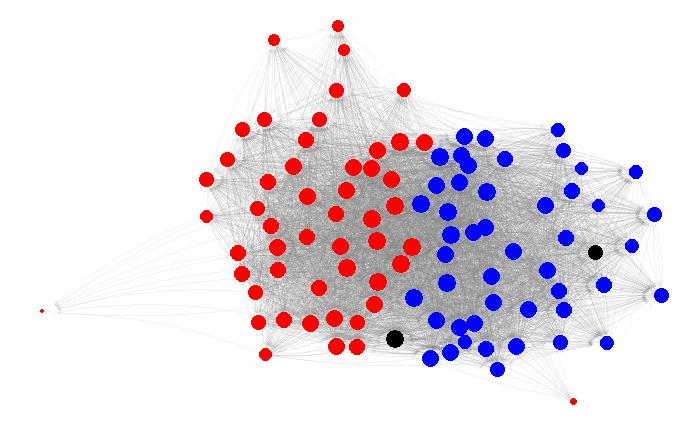
Иерархические алгоритмы бывают:

Агломеративными (восходящими).
Дивизимными (нисходящими).

При работе первых сначала каждый объект является отдельным кластером. Затем они объединяются до размещения всех их в одной группе.

Вторые работают по обратному принципу. Сначала все объекты находятся в одной группе. Затем постепенно разделяются, пока каждый не образует уникальный кластер.

Визуально иерархические алгоритмы представляют с помощью дендрограмм. На таких схемах видна последовательность объединения или разделения объектов.

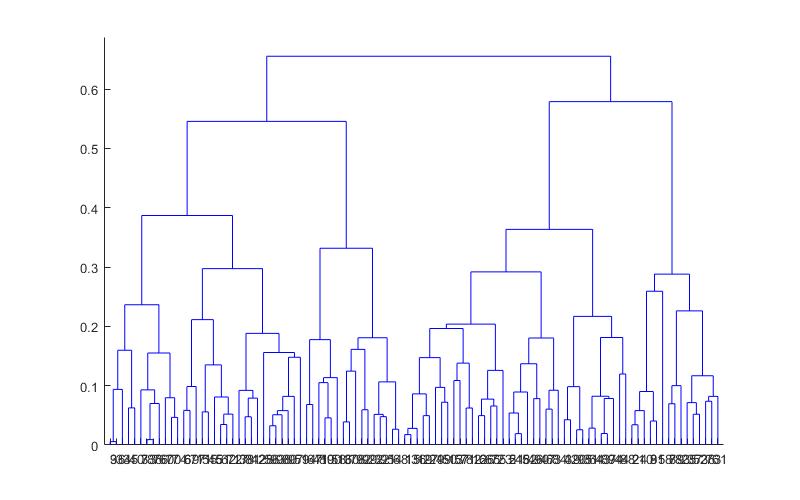
Объединение кластеров

Когда каждый объект является отдельным кластером, расстояния между ними определяются выбранной мерой. При их объединении возникают затруднения в определении расстояния между ними. Поэтому необходимы правила, определяющие порядок этих действий.

Можно связать два кластера, когда два произвольных объекта из разных групп расположены максимально близко друг к другу. В таком случае расстояние определяют по правилу ближайшего соседа или методом одиночной связи. Так создаются волокнистые кластеры (соединенные только отдельными элементами, случайно расположенными рядом).

Метод полной связи или отдаленных соседей заключается в использовании наиболее удаленных объектов в разных группах.

Если расстояние между кластерами определяется как среднее значение между всеми парами объектов в них, применяется метод невзвешенного попарного среднего.

Ему аналогичен метод взвешенного попарного среднего. Отличие между ними лишь в том, что во втором случае размер кластеров используется в качестве весового коэффициента. По этой причине такой метод используется, если объемы групп различается.

При невзвешенном центроидном расчете берется расстояние между центрами тяжести кластеров.

Взвешенный центроидный метод (медиана) похож на предыдущий. Отличие в том, что при расчетах учитывают вес для определения различий в размерах кластеров. По этой причине при существенной разнице рациональнее использовать именно такой метод.

Метод Варда отличается от прочих, так как использует принципы дисперсионного анализа для определения расстояний между кластерами. Он сводит к минимуму сумму квадратов для любых двух групп, которые могут быть созданы на каждом этапе. Метод Варда эффективен, однако он стремится создавать кластеры небольшого размера.

Неиерархические алгоритмы

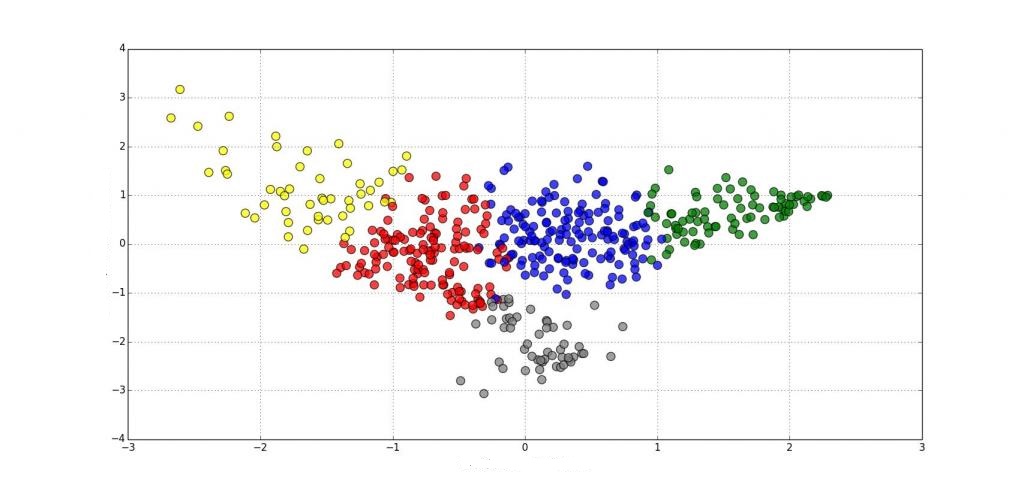
Методы иерархической кластеризации неприменимы при большом количестве наблюдений. Поэтому исследователи обращаются к неиерархической кластеризации.

Наиболее популярный алгоритм K-средних. Метод также именуют быстрым кластерным анализом.

Алгоритм K-средних строит группы, находящиеся на значительных расстояниях друг от друга. Они должны максимально отличаться. Выбор числа K обусловлен результатами ранее проведенных исследований, теоретическими соображениями или интуицией. Метод подходит для анализа небольшого объема данных. К достоинствам относятся:

простота использования;
высокая скорость;
ясность и доступность.

Недостатки:

высокая чувствительность к выбросам, искажающим среднее;
медленная работа с большими базами данных;
потребность задавать число кластеров.

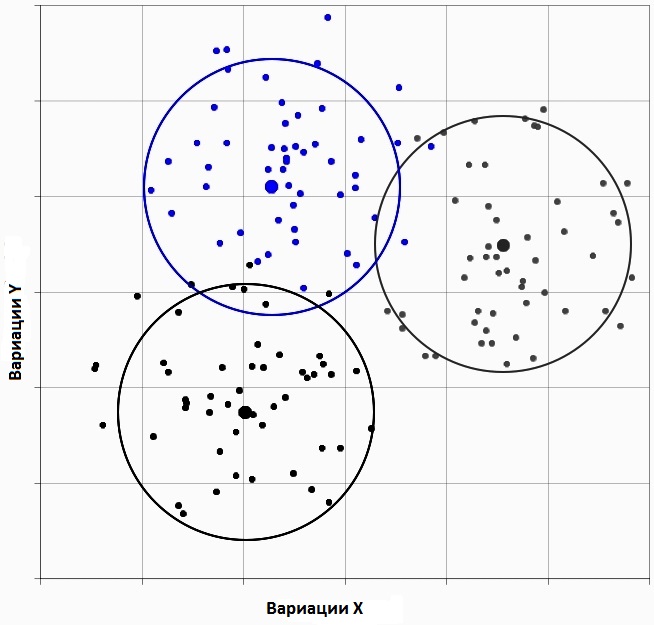
Описание алгоритма K-средних

Сначала объекты распределяются по группам. Далее выбирается число K. На начальном этапе эти точки - центры кластеров. На стадии начальных центроидов может происходить такой выбор:

по результатам K-наблюдений для установления максимального начального расстояния;
случайный;
выбор первых K-наблюдений.

Таким способом все объекты распределяются по конкретным группам.

Итеративный процесс

Центрами становятся покоординатные средние кластеров. Объекты перераспределяются. Этот процесс длится до стабилизации кластерных центров или до достижения максимального числа итераций.

С позиции вычислений метод K-средних является обратным дисперсионным анализом. Работа начинается с K случайно отобранных кластеров. Далее меняется принадлежность объектов к ним для уменьшения изменчивости внутри групп и возрастания этого показателя между ними. В кластеризации данных методом K-средних перемещаются объекты из одних групп в другие. Это нужно выполнять для получения максимально значимого результата при дисперсионном анализе.

Интерпретация результатов

После получения результатов кластеризации методом быстрого анализа рассчитывают средние для каждой группы по каждому измерению. Это выполняется для оценки отличия кластеров друг от друга. Если анализ выполнен качественно, средние значения для большинства групп будут сильно различаться. Значения F-статистики, вычисленные для каждого измерения, это еще один индикатор качества дискриминации кластеров.